One of the wonderful things about mathematics is that it is frequently surprising. Often relatively simple things reveal unexpected hidden depths - and do so with minimal probing. One such aspect of mathematics is the Sierpinski triangle (aka Sierpinski gasket).
The Sierpinski triangle was named after a Polish mathematician who explored the concept around 1915, although it is not true that he “discovered” it as the basic shape apparently appears in art work dating from some centuries before.
The Sierpinski triangle was named after a Polish mathematician who explored the concept around 1915, although it is not true that he “discovered” it as the basic shape apparently appears in art work dating from some centuries before.
The Sierpinski triangle is a self similar set - a pattern that can be made larger or smaller indefinitely while maintaining the same pattern, in other words, it is a fractal. Fractals are not just found on the pages of maths books - which is one of the reasons that they are so fascinating. Fractals are found in many places in nature - from snowflakes to certain leaves, from ferns to forked lightning, even, most unexpectedly, in broccoli. Making Sierpinski triangles is something that even relatively young students can do. Start with an equilateral triangle. Inscribe that triangle with an inverted copy of itself (or, more simply, make an upside down triangle inside the first one). And keep repeating. (One set of instructions for use with young mathematicians can be found here.) The pattern created, as depicted above, is surprisingly pleasing for what is essentially a mathematical process.
Creative types have added colour, and combined them to make them even more so as shown here. So, the Sierpinski triangle is interesting and visually attractive in its own right...but there are some fascinating attributes that do not immediately meet the eye. (Source)
Creative types have added colour, and combined them to make them even more so as shown here. So, the Sierpinski triangle is interesting and visually attractive in its own right...but there are some fascinating attributes that do not immediately meet the eye. (Source)
The other famous triangle in mathematics is Pascal’s triangle. It has become customary to credit the discovery of this triangle to Blaise Pascal although the concept was known well before
him. In Pascal’s triangle the two numbers above a cell are added to create the number in the next row and the process repeats. Now, this is where things get interesting. If we shade only the odd numbers in Pascals triangle we get … something VERY similar to Sierpinski’s triangle - and the similarity strengthens as the larger the triangle continues.

Why might this be?
Sierpinski and Chaos
There is a fascinating game invented by Michael Barnsley called “The Chaos Game” - which, ironically, proves that order can come where chaos is expected.
To “play” this game grab a sheet of paper and mark three points of an equilateral triangle. Label the points A, B and C. Make a mark at any random point on the paper - call it X. Use a die - numbers 1 & 2 relate to point A, 3 & 4 to point B and 5 & 6 to point C. In our example imagine you roll a 1 (which therefore indicates point A). Measure half the distance from P to A and make a new mark. This is the next point. Roll again and mark the point half way between the relevant point indicated by the die and the last point obtained. Repeat and repeat...and repeat. The longer you “play” the game the more strongly a pattern emerges - and that pattern is the Sierpinski triangle!
When I first read about this years ago I wasted hours “playing” the game in an attempt to test it. It proved to be true. These days actually playing the game is not strictly necessary as there are any number of interactive versions of the game available on the Internet. One can be found here - I recommend that you try it for yourself. Concentrate on your sense of wonderment as the patten unfolds. This is the feeling that we want our students to have when they explore mathematics. Incidentally, this “game” has been called the “Creationist’s worse nightmare” - for those who like their maths flavoured with mysticism - and the site that uses the term explains why the pattern works well.
Counter-intuitive results such as that produced by the Chaos game can intrigue students - which leads to engagement...which leads to learning.
Tower of Sierpinski?
For me personally this is perhaps the most perplexing of the unexpected appearances of the Sierpinski triangle.
The Towers of Hanoi is a popular game / puzzle where the player is required to shift a number of disks from one of three “posts” to another of the three available and reassemble them in order with the largest disk at the bottom and the rest of the disk sitting on the bottom disks in order. It is a surprisingly simple yet engrossing game. An interesting thing occurs when the moves leading to a solution of the Towers of Hanoi are graphed.
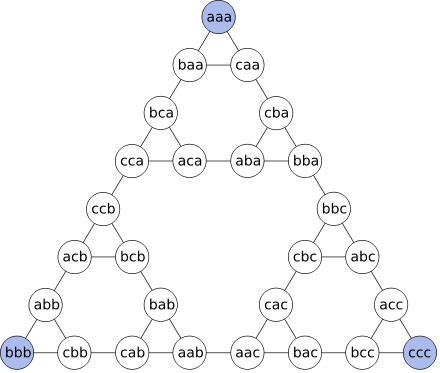 (source)The resemblance of this graph to the Sierpinski triangle is startling. It is worth pausing a moment to think about this. The Tower of Hanoi is a mental experiment, a “game” devised by a human. It is not a “naturally occurring” phenomena such as a fractal snowflake or a symmetrical fern leaf - it is totally the product of human imagination. Yet the solution to this totally invented game, when graphed, has a strong resemblance to the Sierpinski triangle - which is a fractal. It could be argued that Sierpinski triangle is also the product of the human mind - yet this does not diminish the sense of surprise when the link between the two concepts is established. Why should this link exist? The sense that there is some intriguing connection between two such different things is tantalising. In mathematics the enjoyment is in the exploration and the discovery. Sometimes no answer is much more satisfying than a clinical definition that puts everything in its place.Credits:
(source)The resemblance of this graph to the Sierpinski triangle is startling. It is worth pausing a moment to think about this. The Tower of Hanoi is a mental experiment, a “game” devised by a human. It is not a “naturally occurring” phenomena such as a fractal snowflake or a symmetrical fern leaf - it is totally the product of human imagination. Yet the solution to this totally invented game, when graphed, has a strong resemblance to the Sierpinski triangle - which is a fractal. It could be argued that Sierpinski triangle is also the product of the human mind - yet this does not diminish the sense of surprise when the link between the two concepts is established. Why should this link exist? The sense that there is some intriguing connection between two such different things is tantalising. In mathematics the enjoyment is in the exploration and the discovery. Sometimes no answer is much more satisfying than a clinical definition that puts everything in its place.Credits:
Sierpinski triangle image link: http://upload.wikimedia.org/wikipedia/en/thumb/8/88/Sierpinski_Triangle.svg/220px-Sierpinski_Triangle.svg.png Sierpinski hexagon image link: http://ecademy.agnesscott.edu/~lriddle/ifs/siertri/siertri.htm
Pascal/ Sierpinki triangle link: http://www.texample.net/media/tikz/examples/PNG/pascals-triangle-and-sierpinski-triangle.png
Why might this be?
Sierpinski and Chaos
There is a fascinating game invented by Michael Barnsley called “The Chaos Game” - which, ironically, proves that order can come where chaos is expected.
To “play” this game grab a sheet of paper and mark three points of an equilateral triangle. Label the points A, B and C. Make a mark at any random point on the paper - call it X. Use a die - numbers 1 & 2 relate to point A, 3 & 4 to point B and 5 & 6 to point C. In our example imagine you roll a 1 (which therefore indicates point A). Measure half the distance from P to A and make a new mark. This is the next point. Roll again and mark the point half way between the relevant point indicated by the die and the last point obtained. Repeat and repeat...and repeat. The longer you “play” the game the more strongly a pattern emerges - and that pattern is the Sierpinski triangle!
When I first read about this years ago I wasted hours “playing” the game in an attempt to test it. It proved to be true. These days actually playing the game is not strictly necessary as there are any number of interactive versions of the game available on the Internet. One can be found here - I recommend that you try it for yourself. Concentrate on your sense of wonderment as the patten unfolds. This is the feeling that we want our students to have when they explore mathematics. Incidentally, this “game” has been called the “Creationist’s worse nightmare” - for those who like their maths flavoured with mysticism - and the site that uses the term explains why the pattern works well.
Counter-intuitive results such as that produced by the Chaos game can intrigue students - which leads to engagement...which leads to learning.
Tower of Sierpinski?
For me personally this is perhaps the most perplexing of the unexpected appearances of the Sierpinski triangle.
The Towers of Hanoi is a popular game / puzzle where the player is required to shift a number of disks from one of three “posts” to another of the three available and reassemble them in order with the largest disk at the bottom and the rest of the disk sitting on the bottom disks in order. It is a surprisingly simple yet engrossing game. An interesting thing occurs when the moves leading to a solution of the Towers of Hanoi are graphed.
Sierpinski triangle image link: http://upload.wikimedia.org/wikipedia/en/thumb/8/88/Sierpinski_Triangle.svg/220px-Sierpinski_Triangle.svg.png Sierpinski hexagon image link: http://ecademy.agnesscott.edu/~lriddle/ifs/siertri/siertri.htm
Pascals triangle link: http://t3.gstatic.com/images?q=tbn:ANd9GcQB-3ROtNTJ9abzXUIS0I4zzNQGEk3kCdOacPke7RzNuYJbwyFNkg
Pascal/ Sierpinki triangle link: http://www.texample.net/media/tikz/examples/PNG/pascals-triangle-and-sierpinski-triangle.png



No comments:
Post a Comment